Evaluación de la intervención que puede haber tenido el azar en las pruebas imparciales
La intervención del azar puede llevarnos a cometer dos tipos de errores al interpretar los resultados de las comparaciones imparciales de los tratamientos: es posible que concluyamos erróneamente que existen diferencias reales en los resultados de los tratamientos cuando no las hay, o que no existen diferencias cuando las hay. Cuanto más grande sea el número de resultados del tratamiento de interés observados, menor será la probabilidad de que se llegue a conclusiones erróneas de esta manera.
Debido a que las comparaciones de tratamientos no pueden incluir a todas las personas que han padecido o padecerán la enfermedad en cuestión, nunca será definitivamente posible encontrar «las verdaderas diferencias» entre los tratamientos. En cambio, los estudios deben realizar las mejores estimaciones de cuáles serán probablemente las verdaderas diferencias.
La fiabilidad de las diferencias estimadas generalmente se indicará mediante los «intervalos de confianza (IC)». Estos dan el margen dentro del cual probablemente residen las diferencias verdaderas. La mayoría de las personas ya debe estar familiarizada con el concepto de intervalos de confianza, aunque no sea por ese nombre.
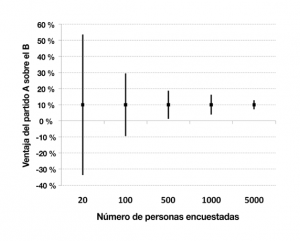
El intervalo de confianza (IC) del 95 % para la diferencia entre los partidos A y B se estrecha a medida que el número de personas encuestadas aumenta (presiona para agrandar)
Por ejemplo, en las vísperas a una elección, una encuesta de opinión puede informar que el partido A está 10 puntos porcentuales por encima del partido B; pero, a menudo, el informe destacará que la diferencia entre los partidos podría ser tan solo de 5 puntos o hasta de 15 puntos. Este «intervalo de confianza» indica que la diferencia verdadera entre los partidos probablemente se encuentra en algún lugar entre 5 y 15 puntos porcentuales
Cuanto más grande sea el número de personas encuestadas, menor será la incertidumbre sobre los resultados y, por lo tanto, más estrecho será el intervalo de confianza asociado con la estimación de la diferencia.
Del mismo modo en que se puede evaluar el grado de incertidumbre en torno a una diferencia estimada en las proporciones de votantes que apoyan a dos partidos políticos, también se puede evaluar el grado de incertidumbre en torno a una diferencia estimada en las proporciones de pacientes que mejoran o empeoran después de dos tratamientos.
Y nuevamente, cuanto más grande sea el número de resultados del tratamiento observados, por ejemplo, la recuperación después de un ataque cardíaco, en una comparación de dos tratamientos, más estrechos serán los intervalos de confianza relativos a las estimaciones de las diferencias de los tratamientos. Cuando se trata de intervalos de confianza, «cuanto más estrechos, mejor».
Por lo general, un intervalo de confianza está acompañado por una indicación de qué tan seguros se puede estar de que el valor verdadero se encuentra dentro del margen de estimaciones presentadas. Por ejemplo, un «intervalo de confianza del 95 %» significa que se puede estar un 95 % seguro de que el valor verdadero de lo que sea que se esté calculando se encuentra dentro del margen del intervalo de confianza. Es decir que hay una probabilidad de 5 en 100 (5 %) de que, en efecto, el valor «verdadero» esté fuera del intervalo.
